En los últimos cursos de la secundaria aparecen unas funciones matemáticas nuevas para nosotros hasta ese momento y que nos trae de cabeza a más de uno: las derivadas.
Nos las presentan de forma geométrica como la pendiente de la recta tangente a una función
en un punto acompañada de:
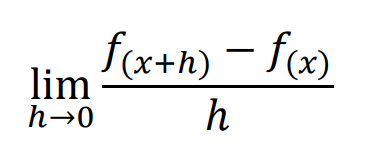
Y tras ver eso, nos presentan una tabla con varias definiciones de derivadas dependiendo de la función que se nos presente para calcular los intervalos de crecimiento, decrecimiento, puntos máximos y mínimos, intervalos de concavidad y convexidad, puntos de inflexión…
Índice del artículo
¿Para qué sirven las derivadas?
Pero hay una pregunta que nos hemos hecho todos en algún momento y es: ¿Para qué sirve todo esto realmente?
La derivada también puede definirse como la rapidez con la que varía una función según el valor de la variable independiente.
👉Consulta nuestros niveles:
Ejemplos sencillos de la aplicación de las derivadas
Un ejemplo que tenéis sobre el papel en la misma asignatura de matemáticas es el cálculo del área, ya que esta es la derivada del volumen. Pero podemos trasladarnos a otras asignaturas como física, donde vemos que, a partir de la posición, podemos obtener la velocidad y la aceleración instantánea a través de la derivada en función del tiempo.
Si extrapolamos todo esto a cosas cotidianas podemos encontrar derivadas en el desgaste de un neumático, el beneficio que tiene una empresa e incluso lo que se propaga un rumor en cierto tiempo.
Las derivadas han sido, y son a día de hoy indispensables para incontables disciplinas, algunos ejemplos son:
Aplicaciones en la medicina:
Las derivadas han sido la clave para poder estudiar la evolución de las enfermedades ya que gracias a ellas podemos estudiar su ritmo de crecimiento y decrecimiento y la efectividad del tratamiento escogido.
Siguiendo la línea, han sido necesarias para estudiar la evolución de las pandemias para poder
estimar el número de enfermos a raíz del tiempo transcurrido.
Aplicaciones en la ingeniería:
Son la base para el diseño de los tratamientos de aguas residuales, el estudio de la contaminación y la evolución de esta. Además de ser las protagonistas cuando se trata del análisis de reducción de costes a la hora de fabricar un producto.
Aplicaciones en la economía:
Proporcionan información útil en el estudio de la evolución del índice de la bolsa, el crecimiento o decrecimiento de los beneficios… llegando a poder calcular con ellas los beneficios máximos que puede obtener el empresario. Esto último es lo que conocéis como: optimización.
Estas son solo algunas de las innumerables aplicaciones que tienen las derivadas en nuestra
vida y en el desarrollo de esta.





Deja una respuesta