Los alumnos de matemáticas desde 6º de primaria a 4º de la ESO suelen encontrar dificultades a la hora de resolver problemas de ecuaciones de primer grado. Su problema no es tanto despejar la x, sino traducir el problema en lenguaje matemático, es decir, pasar las palabras a números. Se trata, por tanto, de una cuestión de comprensión lectora, más que matemática.
Índice del artículo
Problemas de ecuaciones de primer grado
Los problemas con ecuaciones de primer grado suelen ser de edades, de averiguar las monedas que hay en un bolsillo, de calcular las dimensiones de una figura, de “dadas tantas patas y tantas cabezas, cuántos animales de cada clase hay” … En todo caso, tendremos una sola incógnita, que deberemos usar para generar las ecuaciones necesarias para la resolución del problema.
👉Consulta nuestros niveles:
Cuando comprendamos las palabras de cada problema, entonces podremos colocar los signos donde corresponda. A parte de la suma y la resta, podemos encontrar expresiones del tipo: el producto (multiplicación), la mitad, o el tercio o una cuarta parte (fracción). En problemas de edades, por ejemplo, aparecen expresiones del tipo “dentro de 10 años” (+10), “hace 5 años” (-5), etc.
Otras expresiones que suele costar traducir son, por ejemplo “un número par” (2x) o “un número impar” (2x-1).
Ejemplo: José tiene 10 años más que su hermana, y dentro de 6 años tendrá el doble de la que entonces tenga esta. ¿Qué edad tiene cada uno?
- Desconocemos la edad de la hermana, a la que llamaremos x.
- Sabemos que José tiene 10 años más, por lo que tiene x+10.
- Dentro de 6 años, supone sumar 6 años a ambas edades, porque el tiempo pasa para ambos:
- José: x+10+6
- Hermana: x+6
| Ahora | Dentro de 6 años | |
| José | X + 10 | X + 10 + 6 |
| Hermana | X | X + 6 |
- Tendrá el doble de la que entonces tenga esta: 2(x+6)
- Entonces, igualamos:
X+10+6=2(x+6)
- Resolvemos los paréntesis:
X+10+6=2x+12
- Todo lo que tiene x a un lado, todo lo que no tiene x al otro lado:
10+6-12=2x-x
- Resolvemos:
4 = x
- No hemos terminado. Ahora tenemos que indicar las edades de José y su hermana, por lo que tenemos que volver a los pasos 1 y 2:
- Desconocemos la edad de la hermana, a la que llamaremos x à 4 años.
- Sabemos que José tiene 10 años más, por lo que tiene x+10 à 14 años.
Problemas con sistemas de ecuaciones
En ocasiones, tenemos dos incógnitas, pero seguro con alguna relación entre ambas.
Por ejemplo: en una granja hay patos y conejos (dos incógnitas, x e y); entre todos los animales suman 39 cabezas (como cada animal tiene sólo una cabeza, sabemos que x + y = 39). También sabemos que hay 126 patas, y como los patos tienen 2 patas y los conejos 4, así que sabemos también que 2x + 4y = 126. Este sistema lo podremos resolver por sustitución, igualación y reducción.
Problemas de ecuaciones de segundo grado
Hay dos tipos de problemas que incluyen ecuaciones de segundo grado: aquellos en los que contamos con valores para a, b y c (ecuaciones de segundo grado completas); o valores para a y b o a y c (incompletas).
Problemas con ecuaciones incompletas
Estos problemas incrementan un poco su dificultad a la hora de resolverlos, pero son más fáciles de traducir al lenguaje algebraico. Se trata de problemas como “cuál es el número cuyos ¾ más 9, multiplicado por los ¾ menos 9, dan por producto 943”
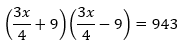
En este caso, deberemos aplicar una de las identidades notables, concretamente la de suma por diferencia. Entonces, tendremos que resolver la siguiente ecuación:
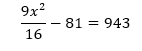
Problemas con ecuaciones completas
En este caso, podremos obtener una ecuación que contenga valores para a, b y c, y aplicaremos entonces la fórmula de la resolución de ecuaciones de segundo grado:
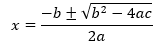
Ejemplo: el área de un cuadrado de lado (4x-1) es 49. Determina el perímetro del cuadrado.
- Sabemos que el área de un cuadrado el lado al cuadrado. Es decir,
(4x-1) (4x-1) = 49
- Resolvemos primero los paréntesis (como siempre):
16x2 – 4x – 4x +1 = 49
16x2 – 8x + 1 = 49
- Igualamos a cero para poder aplicar la fórmula
16x2 – 8x + 1 – 49 = 0





Deja una respuesta