Qué es la «moda» en las matemáticas

Cuando escuchamos la palabra moda lo primero que se nos viene a la cabeza es un desfile en una pasarela, y está bien pero…

¿Qué es la moda en matemáticas? ¿qué significa?

Pues la moda en matemáticas no es más que “lo que se lleva”. Es decir, el valor que más se repite dentro de un conjunto de datos, veámoslo en un ejemplo.

Ejemplo

Se anotan las canastas anotadas por un jugador de baloncesto en 10 partidos:

0, 1, 1, 1, 2, 2, 3, 3, 4, 6

En este ejemplo el valor que más se repite, es decir, el de mayor frecuencia . Tenemos entonces que la moda es 1.

Moda bimodal y multimodal

¿Pero qué pasa si hay más de un valor que se repite más veces que el resto? En este caso diremos que la moda es bimodal si hay dos valores y multimodal si posee más.

Hasta ahora hemos visto cómo se puede calcular la moda de un conjunto de datos . Veamos cómo hacer para cuando tenemos los datos agrupados en intervalos de la misma longitud.

Fórmula de la moda con datos agrupados en intervalos de una misma longitud

Para ello tenemos que aplicar la fórmula:

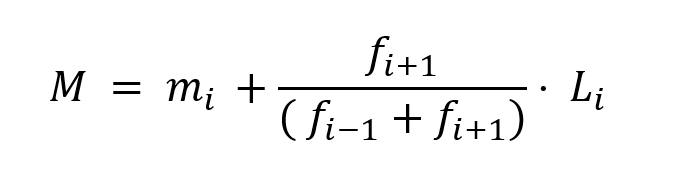
Donde:

m es la moda.

m_i es el límite inferior del intervalo con mayor frecuencia.

f_i+1 es la frecuencia posterior al intervalo con mayor frecuencia.

f_i es la mayor frecuencia.

f_i-1 es la frecuencia anterior al intervalo con mayor frecuencia.

L_i es la longitud del intervalo con mayor frecuencia.

Veamos ahora un ejemplo con valores:

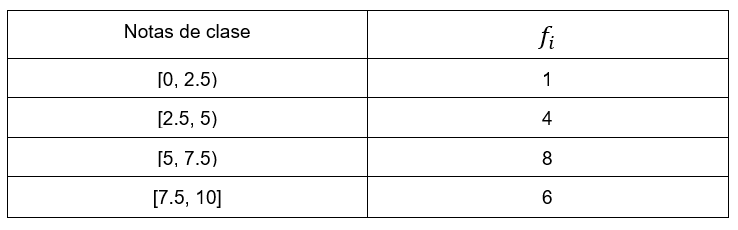
Aplicando la fórmula anterior a esta tabla obtenemos que la moda es

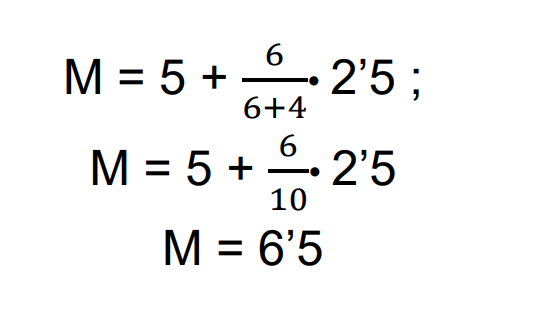
Esto que acabamos de ver es una aproximación bastante buena sobre la moda, pero si queremos ser aún más precisos podríamos usar la siguiente fórmula:

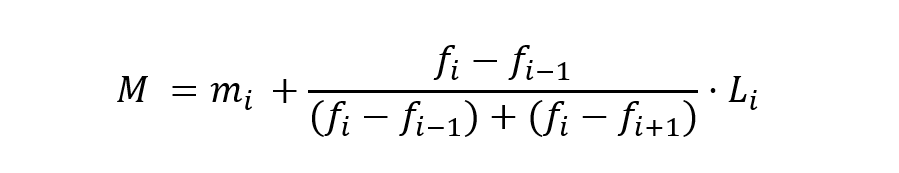
Para el último ejemplo visto tendremos que la moda es:

Ya hemos visto cómo podemos calcular la moda en un conjunto de datos sueltos y en un conjunto de datos agrupados en intervalos de misma longitud. Pero, ¿qué pasa si la longitud de los intervalos es distinta para cada intervalo?. En este caso aplicaremos una fórmula similar a las anteriores en las que necesitaremos calcular las alturas de los intervalos, a las que llamaremos h_i.

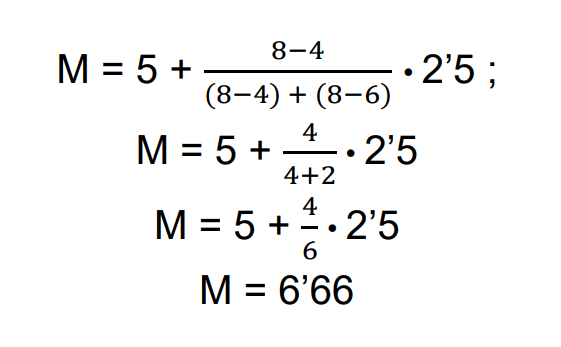
El cálculo de las alturas será:

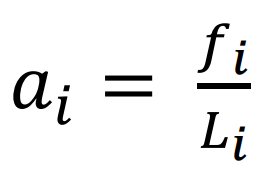
Y las fórmulas para calcular la moda será:

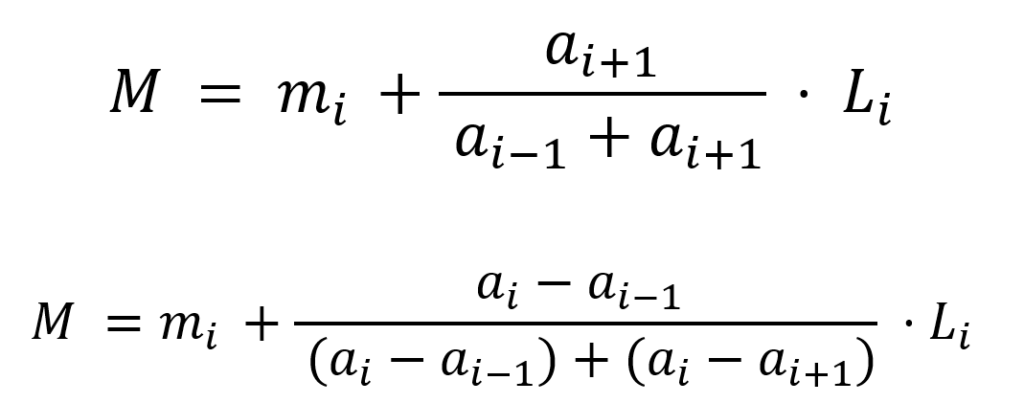
Donde

m es la moda

m_i es el límite inferior del intervalo con mayor altura.

a_i+1 es la altura posterior al intervalo con mayor altura.

a_i es la mayor altura.

a_i-1 es la altura anterior al intervalo con mayor altura.

L_i es la longitud del intervalo.

Si tenemos la siguiente tabla:

Si queremos calcular la moda de forma más sencilla aplicamos la primera fórmula, obteniendo:

Mientras que si queremos una aproximación mejor de la moda aplicamos la segunda:

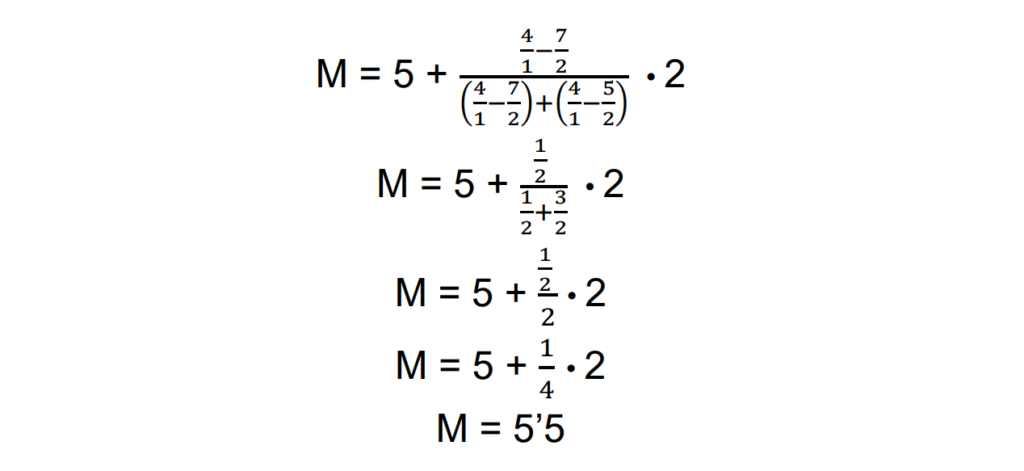
Si queréis preguntar o decir algo más sobre la moda en las matemáticas, os esperamos en los comentarios.