La R.A.E. define ecuación como: “Igualdad que contiene una o más incógnitas”.
Las ecuaciones acompañan a los alumnos a lo largo de todos sus estudios en la ESO, Bachillerato, universidad… en asignaturas tales como matemáticas, física, economía, tecnología… están presentes en nuestro día a día, en situaciones cotidianas, aunque en la mayoría de los casos no nos demos cuenta. Cuando calculamos el precio de una camiseta que vamos a comprar con descuento, al calcular cuánto nos toca pagar en una cena con amigos, a cuantos trozos de pizza tocamos… todo ello lo calculamos mediante la resolución de una ecuación.
Las ecuaciones son el resultado de llevar al lenguaje matemático situaciones de la vida cotidiana.
Índice del artículo
Formas de clasificar las ecuaciones
Hay distintas formas de clasificar las ecuaciones en función del criterio elegido. A continuación veremos algunas clasificaciones, siendo la más habitual la clasificación en función del tipo de expresiones algebraicas que contiene la ecuación.
Clasificación en función del número de soluciones que puede tener la ecuación
Que no tenga solución
Por ejemplo: x+6=x+2
Que tenga una o varias soluciones.
Por ejemplo:

Que tenga infinitas soluciones.
Por ejemplo:

Clasificación en función del tipo de expresiones algebraicas que contiene la ecuación
Ecuación polinómicas o algebraicas
👉Consulta nuestros niveles:
Ecuaciones de primer grado o lineales
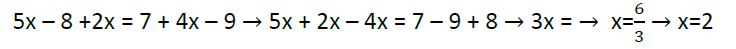
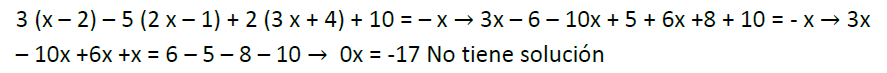
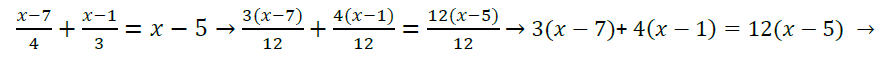
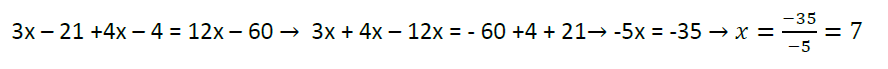
Ecuaciones de segundo grado o cuadráticas.
Pueden se: completas o incompletas
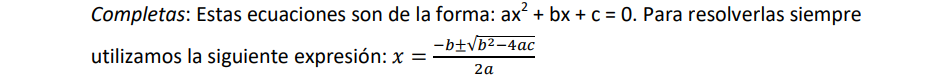
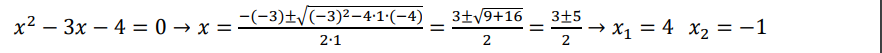

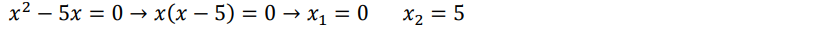

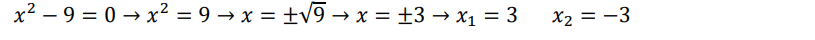
Ecuaciones de tercer grado o cúbicas
Para resolver las ecuaciones de tercer grado vamos a utilizar, generalmente, la regla de Ruffini
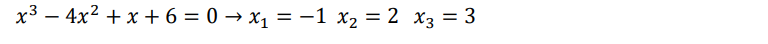
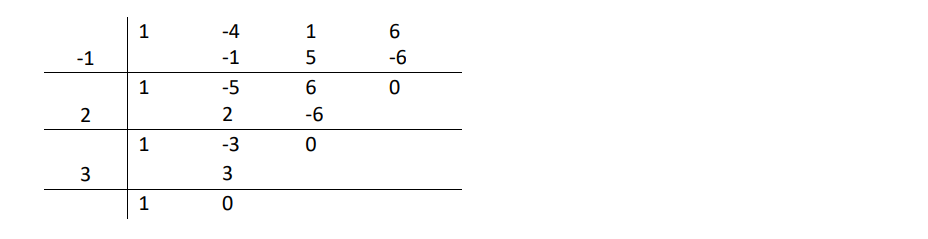
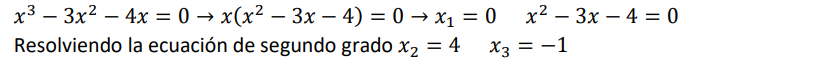
Ecuaciones bicuadradas
Estas ecuaciones son de la forma:
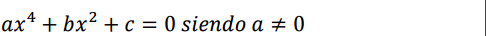
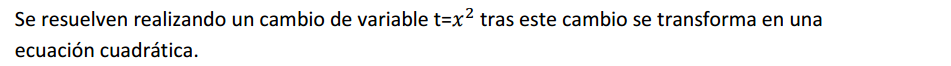
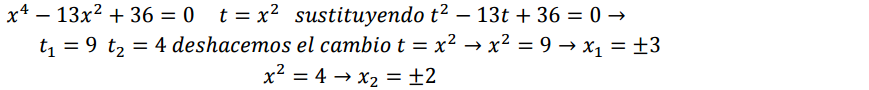
Ecuaciones de grado n
Para resolver estas ecuaciones vamos a utilizar, generalmente, la regla de Ruffini.
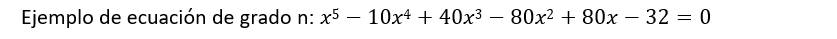
Ecuaciones racionales
Para resolver este tipo de ecuaciones calculamos el m.c.m. de los denominadores y reducimos a común denominador. Si tenemos cociente a ambos lados del igual podemos multiplicar directamente en cruz.
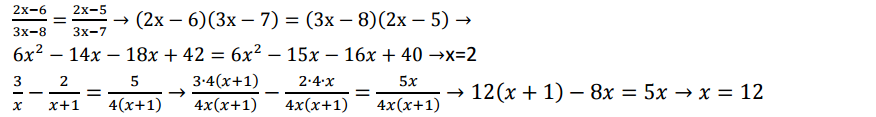
Ecuaciones irracionales
Para resolver este tipo de ecuaciones elevamos al cuadrado a cada lado del igual. Recuerda:
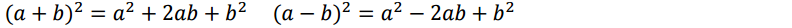
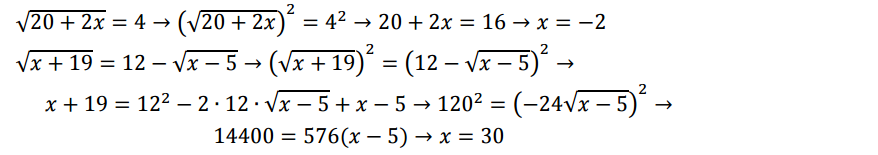
Ecuación no polinómica
Ecuaciones diferenciales
Una ecuación diferencial es una ecuación que incluye expresiones o términos que involucran a una función matemática incógnita y sus derivadas. Ejemplo:

Ecuaciones trigonométricas
Son ecuaciones en las que la incógnita aparece en una función trigonométrica (normalmente en el seno, el coseno o la tangente). Para resolver una ecuación trigonométrica haremos las transformaciones necesarias para trabajar con una sola función trigonométrica, para ello utilizaremos las identidades trigonométricas fundamentales.
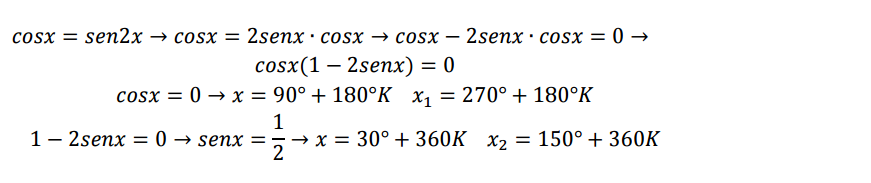
Ecuaciones logarítmicas
Son ecuaciones que tienen logaritmo en uno o en los dos lados del igual y la incógnita forma parte del argumento del logaritmo. Para resolverlas se aplican las propiedades de los logaritmos.
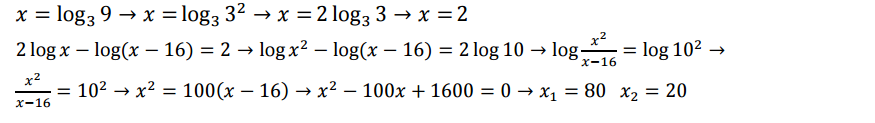
Ecuaciones exponenciales
Son ecuaciones en las cuales la incógnita aparece en los exponentes de potencias de base constante únicamente, en uno o varios términos.
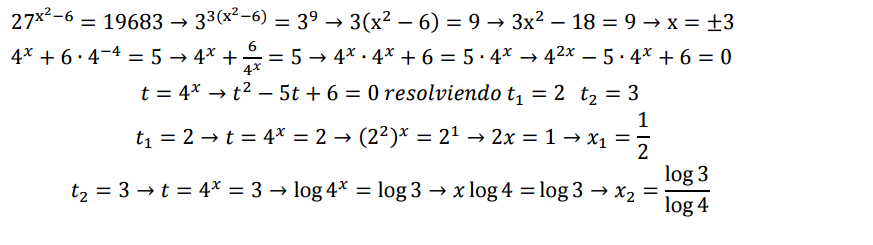
Ecuaciones integrales
Aquella en que la incógnita se encuentra en el integrando.





Me ha servido mucho, en lo que a matemáticas se refiere, gracias por ayudar
Hola Ángel:
Nos alegramos que te haya ayudado en tu aprendizaje. Gracias por decírnoslo.
Un saludo
Buenos días mi hija tiene q resol era ecuaciones q tienen resultado pero no tiene números en las operaciones no tenes idea como resolver
Hola Karen.
En el caso que me comentas, habría que operar como si las letras fuesen números, dejando la incógnita a un lado, y las letras al otro. Se resolvería por el mismo procedimiento. No obstante, te animamos a pasarte por alguna de nuestras sedes para que podamos ayudarte.
Un saludo.
Por favor, que libro me recomiendan para estudiar todo lo relacionado con ecuaciones. Gracias y feliz dia
Hola Jesús, puedes pasarte por cualquiera de nuestras sedes para que podamos asesorarte. Un abrazo.
wow me ayudo mucho, por que explica y a la vez te da ejemplos
¡Gracias Ángel!