Cuando estamos acabando 2ºBachillerato, con el agua al cuello, deseando que pase ya el
infierno, nos presentan a estas pequeñas amiguitas. Si ya nos cuesta lidiar con las
derivadas, aparecen las integrales. Pues bien, con esta pequeña guía vamos a aprender, al
menos, a diferenciar los tipos de integrales para poder resolverlas. Y es que una de las tareas más complicadas es saber distinguir el tipo de integral que intentamos resolver.
Índice del artículo
Integrales inmediatas
Las integrales inmediatas, como su propio nombre indica, son aquellas que se pueden
resolver directamente, mediante una tabla de integración ya estipulada. No necesitan
ninguna transformación previa, salvo la utilización de las propiedades de las integrales, pero
manteniendo la función original.
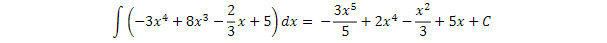
También tenemos las integrales reducibles a inmediatas, que son aquellas en las que
necesitamos calcular la derivada de la función principal para “hacer magia” y que aparezca
dentro de nuestra integral para acabar resolviéndola.
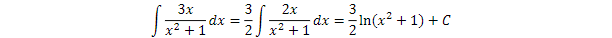
Ejemplo resuelto:
Ejemplo resuelto:
Integrales racionales
Las integrales racionales son aquellas integrales de funciones racionales que no se pueden
resolver de forma inmediata. Y si ya era complicado en este punto, agárrate. Distinguimos
entre dos casos distintos:
● Cuando el numerador es de mayor o igual grado que el denominador. En este primer
caso se resuelve tan fácil como dividir el numerador entre el denominador, quedando
el cociente más el resto entre el denominador. Este último término es inmediato o del
segundo caso.
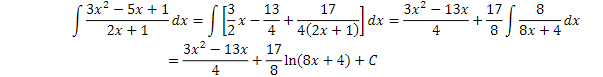
● Cuando el numerador tiene menor grado que el denominador. Aquí ya puedes
empezar a llorar un poco. Se factoriza el denominador y es como meterte en el
Delorian, haces el m.c.m. hacia atrás. Igualas tu numerador original a la suma de los
nuevos (A y B) y sustituyes la “x” en los puntos que hacen que, mágicamente, se te
simplifique el resultado. En este punto ya deberías tener integrales inmediatas y
dejarás de llorar a regañadientes.
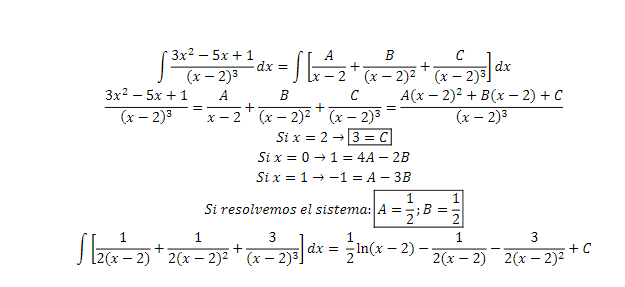
Ejemplo resuelto:
Integrales por partes
Darse cuenta de que tienes delante una integral por partes es difícil pero, una vez lo
identificas, ya crees que todas son así. Las integrales por partes son aquellas no inmediatas
donde se multiplican dos funciones: una fácil de integrar y otra fácil de dividir. No olvides la
regla del soldado: “Sergio un día vio un valiente soldado vestido de uniforme”.
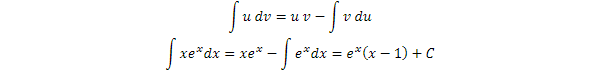
Ejemplos resueltos
Integrales por sustitución
El último tipo de integral de esta guía de supervivencia contra las integrales son las
integrales por sustitución o cambio de variable. Cuando no te viene bien una función un
poco complicada que esté en función de “x”, se cambia por una función más simple en
función de otra variable. Y parece “fácil” pero de fácil no tiene absolutamente nada. A veces
identificar el cambio de variable es tan complicado como intentar resolverlo sin hacerlo.
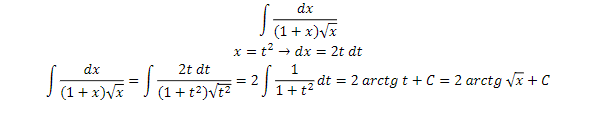
👉Consulta nuestras academias:





Deja una respuesta